Довженко Н.П.
Цель проекта
Содержание
1. Входящий контроль. Спецификация для учителя
2. План работы
3. Инструкция для учащихся по выполнению работы
4. Самостоятельная работа
5. Ответы и решения
6. Текущий контроль. Спецификация для учителя
7. План работы
8. Инструкция для учащихся по выполнению работы
9. Самостоятельная работа
10. Ответы и решения
11. Итоговый контроль. Спецификация для учителя
12. План работы
13. Инструкция для учащихся по выполнению работы
14. Самостоятельная работа
15. Ответы и решения
16. Список литературы
Входящий контроль
Спецификация для учителя.
Цель проверочной работы: проверить готовность учащихся к восприятию и пониманию темы: «Системы линейных уравнений».
Работу целесообразно провести на втором уроке по теме: «Линейное уравнение с двумя переменными» перед изучением темы «График линейного уравнения с двумя переменными». Так как на входящий контроль нецелесообразно тратить целый урок, поэтому работа состоит в основном из заданий с выбором ответов
Задания 1 и 2 контролируют усвоение темы «Линейное уравнение с двумя переменными»
Задание 3 проверяет умение определять, принадлежит ли точка графику функции.
Задание 4 контролирует умение решать линейные уравнения с одной переменной и находить у, если известно значение х. также № 4 можно решить, если ответить на вопрос, принадлежит ли точка двум графикам.
Задание 5 проверяет умение строить график линейной функции. Также это задание можно, выполнить, решив линейное уравнение.
Задание 6 контролирует понимание смысла углового коэффициента прямой.
Задание 7 проверяет умение раскрывать скобки, приводить подобные слагаемые в буквенном выражении, находить значение буквенного выражения при заданном значении переменной
Каждое задание I части оценивается 1 баллом.
Критерии оценивания II части
6 | 2 балла– верное решение, верный ответ |
1 балл – правильно определено k или при нахождении b допущена вычислительная ошибка, а так же если окончательное уравнение прямой не записано | |
0 баллов – любой другой ответ или его отсутствие | |
7 | 3 балла – верное решение, верный ответ |
2 балла – выражение не упрощалось, но ответ подсчитан правильно | |
1 балл – правильно упрощено выражение, но допущена ошибка в вычислении | |
0 баллов – любой другой вариант или отсутствие решения |
План работы
Работа содержит 7 заданий. Рассчитана на 20 минут. В работе 5 заданий базового уровня сложности (Б), 2 задания повышенного уровня (П), 5заданий с выбором ответа (ВО) и 2 задания с развёрнутым ответом (РО).
№ | Раздел содержания | Объект оценивания | Уро-вень слож-ности | Тип зада-ния | Время выполне-ния | Балл за зада-ние |
1 | Линейное уравнение с двумя переменными | Определение понятия | Б | ВО | 1 | 1 |
2 | Линейное уравнение с двумя переменными | Выражение одной переменной через другую | Б | ВО | 2 | 1 |
3 | Линейная функция | Понимание связи координат точки с формулой, задающей функцию | Б | ВО | 2 | 1 |
4 | Составление и решение уравнения | Использование уравнений для нахождения точки пересечения графиков | Б | ВО | 2 | 1 |
5 | Линейная функция, её график | Понимание расположения графика линейной функции в зависимости от значений k и b | Б | ВО | 4 | 1 |
6 | Взаимное расположение двух прямых | Понимание смысла углового коэффициента | П | РО | 4 | 2 |
7 | Преобразование выражений. Числовое значение выражения | Раскрытие скобок, приведение подобных слагаемых, вычисления | П | РО | 5 | 3 |
| Итого |
|
|
| 20 | 10 |
Инструкция по выполнению работы.
В №№ 1 – 5 необходимо выбрать и обвести кружочком правильный ответ, если на вопрос несколько ответов, то обвести эти ответы. Исправить неверный ответ можно, перечеркнув кружочек крест накрест и обведя правильный ответ. За каждое задание ставится 1 балл.
В № 6 и в № 7 необходимо привести решение и записать ответ.
6 задание оценивается 2 баллами, 7 задание 3 баллами
Количество баллов | Оценка |
4 – 5 | 3 |
6 – 7 | 4 |
8 – 10 | 5 |
На выполнение работы отводится 20 минут.
Самостоятельная работа
I часть
1. Какое уравнение не является линейным уравнением с двумя переменными
1) 9х+у=1, 2) 5х – 8у=0, 3) 7х+2у=2, 4) 14у3+6х=8. [5, с.201]
2. В уравнении 2х – у=6 выразите х через у:
1) х= 3+у, 2) х=0,5у – 3, 3) х=0,5у+3, 4) у=2х – 6. [2, с.50]
3. Какие из точек принадлежат графику функции, заданной формулой
у=– 3х+1.
1) (2;7), 2) (– 2;7), 3) (– 2;5), 4) (2;– 5).
4. Не выполняя построения, найдите координаты точки пересечения графиков функций у=3х – 4 и у=5х+14. [6, с.42]
1) (9;23), 2) (– 9;–31), 3) (5;11), 4) (– 5;– 19).
5. В какой координатной четверти находится точка пересечения графиков
у=– 3х и у=3х – 6:
1) I 2) II 3) III 4) IV. [2, с.50]
II часть
6. Составьте уравнение прямой, проходящей через точку А(2;–1) параллельно прямой у=2х. [6, с.100]
7. Упростите выражение 2b – 3(10b – 1)+2(4b – 1) и вычислите его значение при b= – 0,1. [7, с.82]
Ответы № 1 – 5
1 | 2 | 3 | 4 | 5 |
4 | 3 | 24 | 2 | 4 |
Решение заданий № 6;7
№ 6.
у=kх+b, параллельно у=2х через А(2;–1)
k=2, т.к. у параллельных прямых угловой коэффициент одинаковый. Подставим в уравнение координаты точки А вместо х и у, и 2 вместо k.
2·2+b= –1, b= –1 – 4= –5.
Ответ: у=2х – 5.
№ 7. 2b – 3(10b – 1)+2(4b – 1)= 2b – 30b + 3+8b – 2= – 20b+1.
b= – 0,1; – 20·(– 0,1)+1=3.
Ответ: 3.
Текущий контроль
Спецификация для учителя
Цель самостоятельной работы: проверить усвоение темы «Решение систем линейных уравнений», оценить способность применять в дальнейшем учащимися различные способы решения систем в том числе и для решения задач практического содержания.
Работу следует провести после изучения всех трёх способов решения систем линейных уравнений. В работе используются три типа заданий: с выбором ответа, с кратким ответом и с развёрнутым ответом.
Задание 1 проверяет умение определять, является ли пара чисел решением уравнения с двумя переменными.
Задание 2 контролирует умение находить в уравнении одну переменную, если известно значение другой.
Задание 3 проверяет умение выполнять подстановку.
Задание 4 контролирует умение складывать уравнения почленно.
Задание 5 проверяет умение решать системы способом подстановки (основной способ решения систем).
Задание 6 проверяет умение решать системы способом сложения.
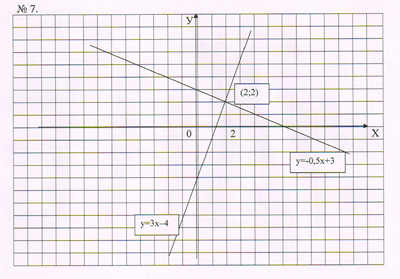
Задание 7 контролирует освоение графического способа решения систем.
Работа состоит из двух частей: I часть состоит из 4 заданий с выбором ответа или кратким ответом, каждое задание оценивается 1 баллом, II часть состоит из 3 заданий, в которых нужно привести полое решение.
Критерии оценивания II части
№ | Критерии оценивания |
5 | 2 балла – верное решение, верный ответ |
1 балл – верное решение, но в ответе вместо (0;1) записано (1;0) | |
0 баллов – любой другой ответ или его отсутствие | |
6 | 2 балла– верное решение, верный ответ |
1 балл – верно найдено значение одной переменной или при вычислении второй переменной допущена вычислительная ошибка | |
0 баллов – любой другой ответ или его отсутствие | |
7 | 3 балла – верное решение, верный ответ |
2 балла – верное построение графиков, но из-за погрешности в построении дан неверный ответ | |
1 балл – правильно построен 1 из графиков | |
0 баллов – любой другой вариант или отсутствие решения |
План работы
Работа содержит 7 заданий. Рассчитана на 30 минут. 2 задания с выбором ответа (ВО) базового уровня (Б), 2 задания с кратким ответом (КО) базового уровня, 1 задания с развёрнутым ответом базового уровня и 2задания с развёрнутым ответом повышенного уровня (П)
№ | Раздел содержания | Объект оценивания | Уро-вень слож-ности | Тип зада-ния | Время выполне-ния | Балл за зада-ние |
1 | Линейное уравнение с двумя переменными | Понятие решения уравнения с двумя переменными | Б | ВО | 2 | 1 |
2 | Линейное уравнение с двумя переменными | Вычисление одной переменной, если известно значение другой | Б | ВО | 2 | 1 |
3 | Подстановка выражений вместо переменных | Понимание смысла подстановки | Б | КО | 3 | 1 |
4 | Алгебраическое сложение двух уравнений | Понимание смысла почленного сложения | Б | КО | 2 | 1 |
5 | Решение системы способом подстановки | Использование способа подстановки для решения систем | Б | РО | 6 | 2 |
6 | Решение системы способом сложения | Использование способа алгебраического сложения для решения систем | П | РО | 5 | 2 |
7 | Решение системы графическим способом | Использование графиков для решения систем | П | РО | 10 | 3 |
| Итого |
|
|
| 30 | 11 |
Количество баллов | Оценка |
4 – 5 | 3 |
6 – 8 | 4 |
9 – 11 | 5 |
На работу отводится 30 минут
Самостоятельная работа
I часть


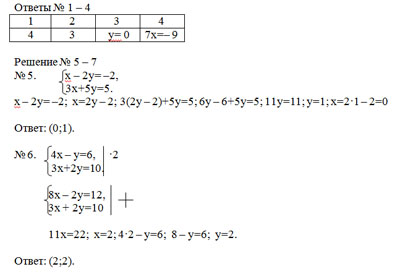

Цель контрольной работы по теме «Системы линейных уравнений:
Проверка усвоения учащимися темы «Системы линейных уравнений», готовности применять данную тему при решении практических задач, готовности решать более сложные системы.
Задание 1 проверяет умение определять, является ли пара чисел решением системы уравнений с двумя переменными.
Задание 2 контролирует умение составлять простейшие системы для решения практических задач.
Задание 3 проверяет умение определять по коэффициентам взаимное расположение прямых.
Задание 4 контролирует умение применять систему линейных уравнений для решения практических задач.
Задание 5 проверяет умение применять системы линейных уравнений для задания линейной функции.
Задание 6 проверяет умение применять изученные способы для решения систем.
Задание 7 проверяет умение применять изученные способы для решения более сложных систем.
Каждое задание I части оценивается 1 баллом.
Критерии оценивания II части
6 | 2 балла– верное решение, верный ответ |
1 балл – ход решения верный, но допущена вычислительная ошибка | |
0 баллов – любой другой ответ или его отсутствие | |
7 | 3 балла – верное решение, верный ответ |
2 балла – система решена методом подбора с доказательством отсутствия других решений | |
1 балл – система решена, но допущена вычислительная ошибка | |
0 баллов – любой другой вариант или отсутствие решения |
План работы
Работа рассчитана на 1 урок с учётом организационного момента. Содержит 7 заданий: 5 базового уровня (Б), из них 3 задания с выбором ответа (ВО), 2 задания с кратким ответом (КО) и 2 задания повышенного уровня (П) с развёрнутым ответом (РО).
№ | Раздел содержания | Объект оценивания | Уро-вень слож-ности | Тип зада-ния | Время выполне-ния | Балл за зада-ние |
1 | Система линейных уравнений | Понятие решения системы | Б | ВО | 2 | 1 |
2 | Текстовая задача практического содержания | Составление двух уравнений с двумя переменными по условию задачи | Б | ВО | 3 | 1 |
3 | Система линейных уравнений | Представление о взаимном расположении двух прямых | Б | ВО | 5 | 1 |
4 | Текстовая задача практического содержания | Применение систем линейных уравнений для решения задачи | Б | КО | 5 | 1 |
5 | Система линейных уравнений | Применение систем линейных уравнений для задания функции | Б | КО | 5 | 1 |
6 | Система линейных уравнений | Использование одного из способов для решения систем | П | РО | 10 | 2 |
7 | Система линейных уравнений с тремя переменными | Применение алгебраических способов для решения систем трёх уравнений с тремя переменными | П | РО | 10 | 3 |
|
|
|
|
| 40 | 10 |
Инструкция для ученика по выполнению работы
В № №1 – 3 необходимо выбрать и обвести кружочком правильный ответ. Исправить неверный ответ можно, перечеркнув кружочек крест накрест и обведя правильный ответ. В № 4 и № 5 дать краткий ответ. Исправить неверный ответ можно, зачеркнув его и рядом написать верный ответ. Задания 1 – 5 оцениваются 1 баллом. В заданиях 6 и 7 привести развернутое решение и дать ответ. № 6 оценивается 2 баллами, № 7 – 3 баллами
Количество баллов | Оценка |
4 – 5 | 3 |
6 – 8 | 4 |
9 – 10 | 5 |
На работу отводится 40 минут


Список использованной литературы.
- М.В. Ткачёва. Алгебра. Тематические тесты, 7. ГИА. Просвещение, 2010г.
- П.В. Чулков и др. Алгебра. Тесты. 7 – 9 класс. ООО «Издат-Школа», 1998г.
- Л.В. Кузнецова и др. Алгебра: сборник заданий для подготовки к итоговой аттестации в 9 классе. Просвещение, 2006г.
- М.Н. Кочагина, В.В. Кочагин. ГИА 2009. Математика: сборник заданий, 9 класс. ООО «Издательство «Эксмо», 2008г.
- В.И. Панарина. Алгебра. 7 класс. 224 диагностических варианта. ООО «Национальное образование», 2012г.
- Н.В.Васюк и др. под ред. П.В. Чулкова. Дидактические материалы по алгебре, 7 класс. ООО «Издат-Школа», 1998г.
- Г.В. Сычева и др. Алгебра. Экспресс-репетитор для подготовки к ГИА. 9 класс. ООО «Издательство Астрель», 2009г.


